
For example, you might compare a control group, with a drug treatment group and a group treated with drug plus antagonist. One-way ANOVA compares three or more groups defined by one factor. Prism does not test for violations of this assumption. While this assumption is not too important with large samples, it can be important with small sample sizes. Furthermore, it assumes that the random component follows a Gaussian distribution and that the standard deviation does not vary between individuals (rows) or treatments (columns). Repeated-measures ANOVA assumes that each measurement is the sum of an overall mean, a treatment effect (the average difference between subjects given a particular treatment and the overall mean), an individual effect (the average difference between measurements made in a certain subject and the overall mean) and a random component. Is the random variability distributed according to a Gaussian distribution?
Since this factor would affect data in two (but not all) rows, the rows (subjects) are not independent. In this case, some factor may affect the measurements from one animal. For example, the errors are not independent if you have six rows of data, but these were obtained from three animals, with duplicate measurements in each animal. You must think about the experimental design. The results of repeated-measures ANOVA only make sense when the subjects are independent. Ideally, your choice of whether to use a repeated-measures test should be based not only on this one P value, but also on the experimental design and the results you have seen in other similar experiments. If the P value for matching is large (say larger than 0.05), you should question whether it made sense to use a repeated-measures test.

Prism tests the effectiveness of matching with an F test (distinct from the main F test of differences between columns). The matching should be part of the experimental design and not something you do after collecting data. By analyzing only the differences, therefore, a matched test controls for some of the sources of scatter. Some factors you don't control in the experiment will affect all the measurements from one subject equally, so will not affect the difference between the measurements in that subject. The whole point of using a repeated-measures test is to control for experimental variability. Read elsewhere to learn about choosing a test, and interpreting the results.
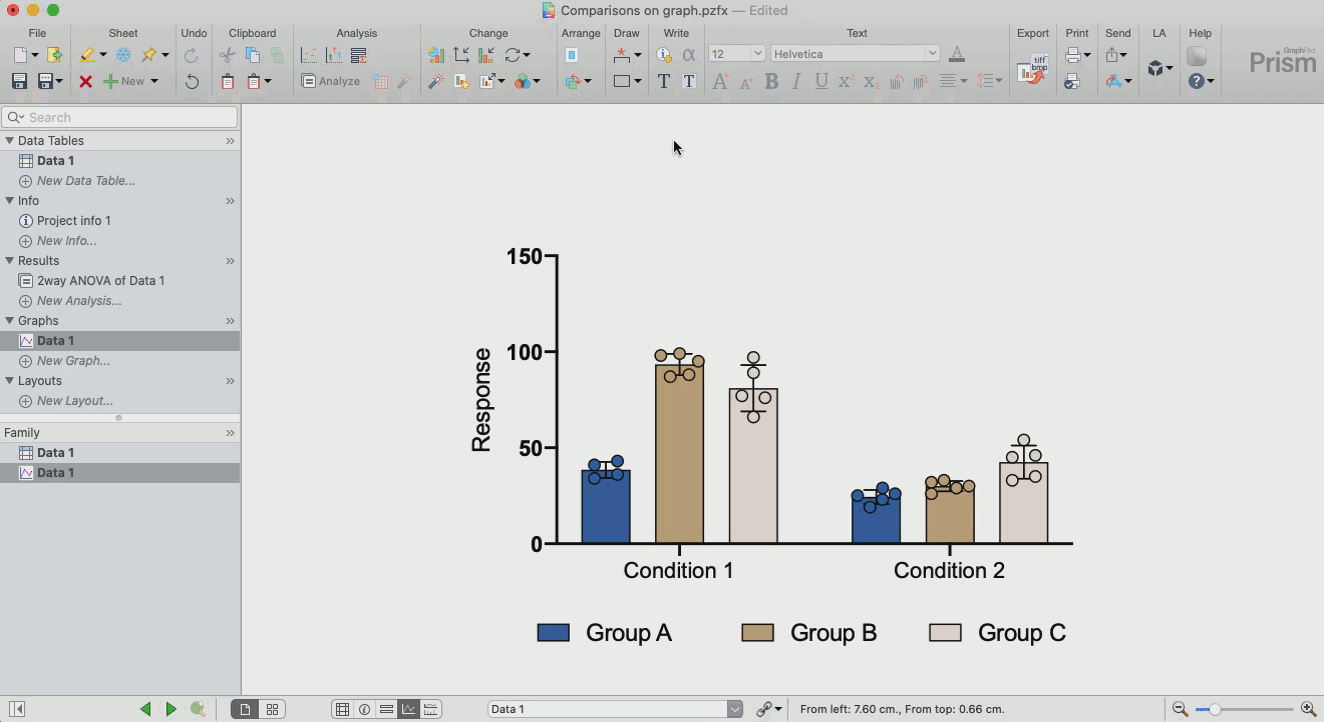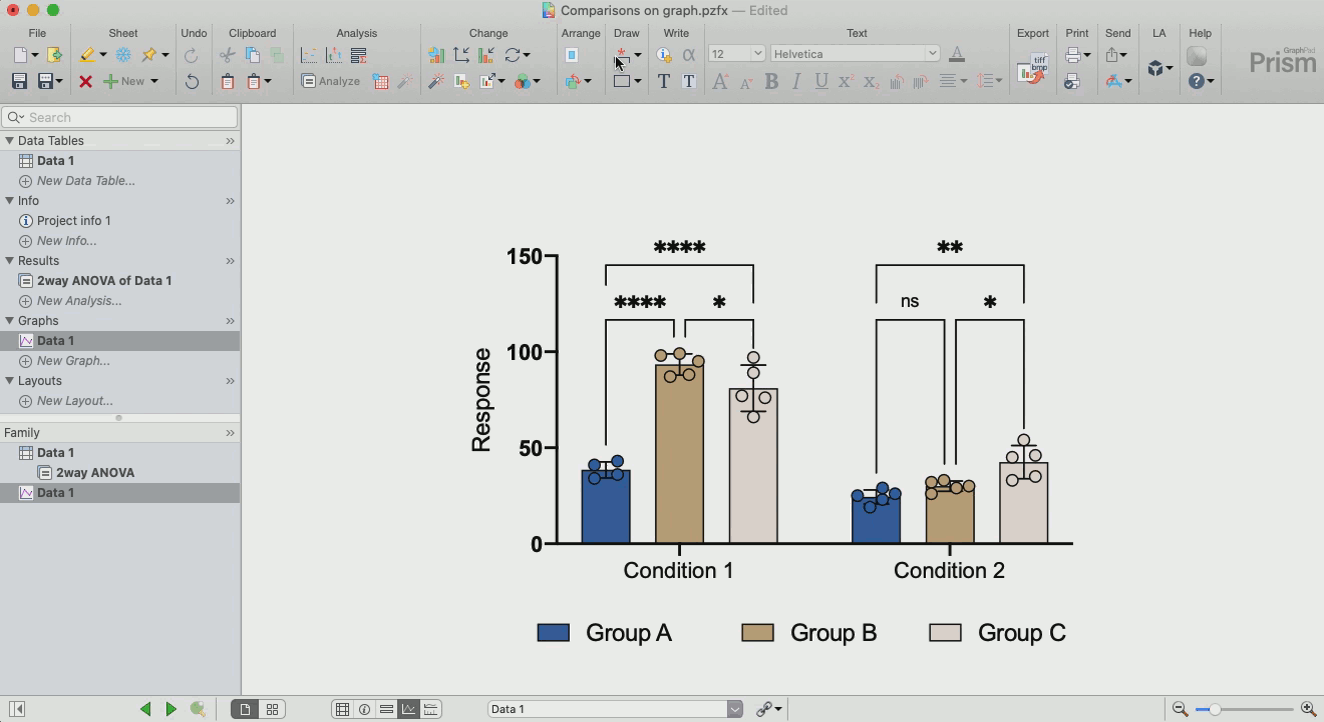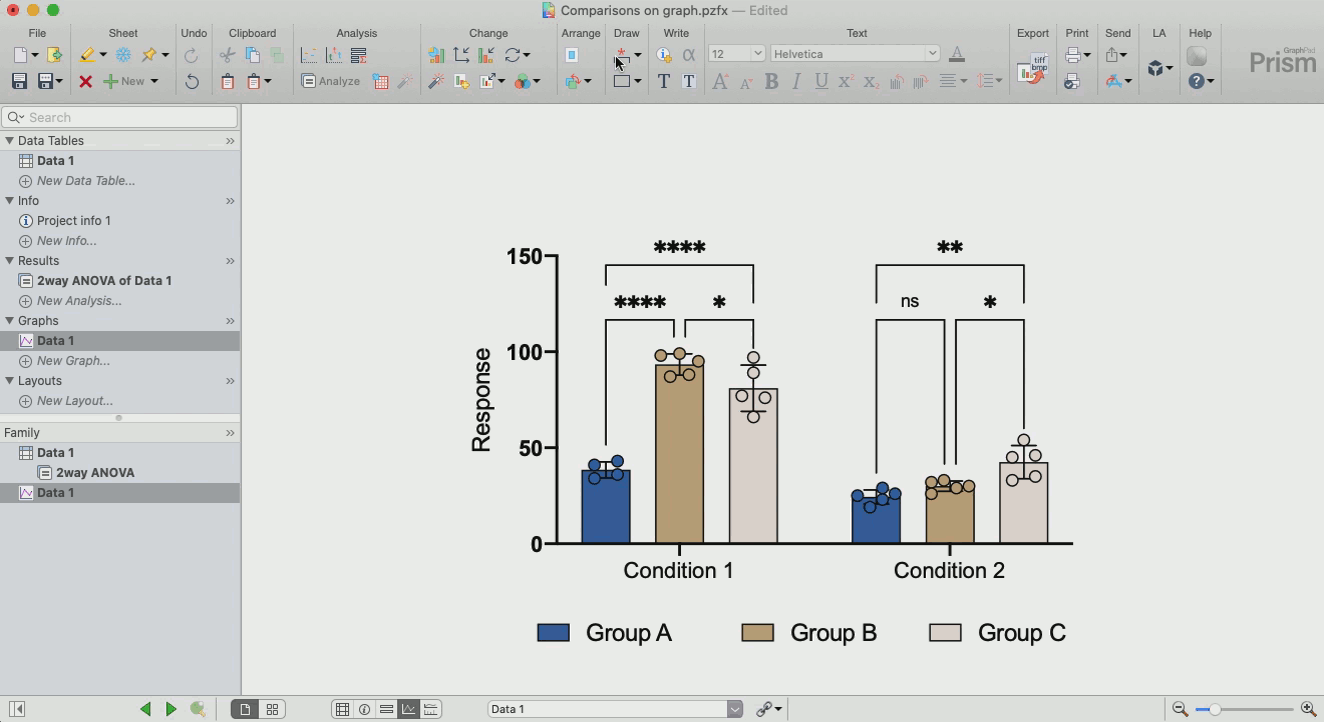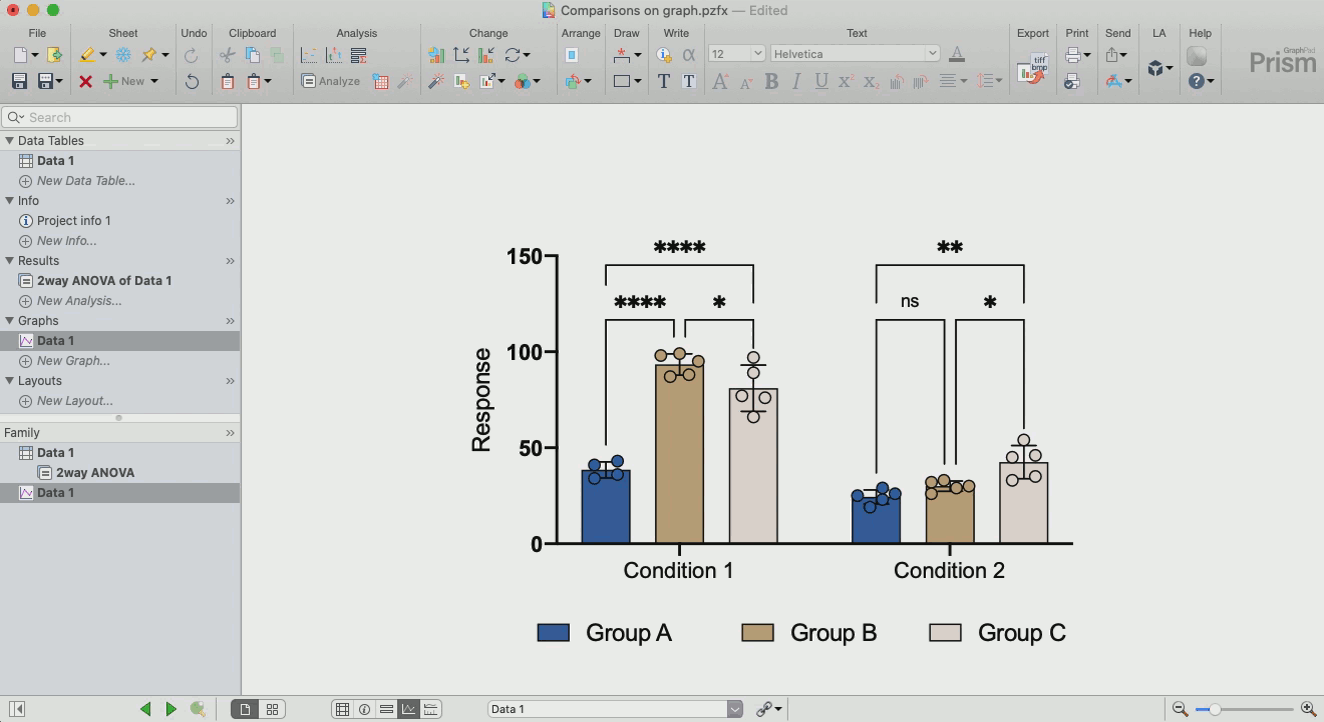
Repeated measures one-way ANOVA compares the means of three or more matched groups.


 0 kommentar(er)
0 kommentar(er)
